Proof of Stake is a fascinating way to describe the consensus protocol used by blockchains like Ethereum, where staked funds replace hash power as the source of security and block production rights.
In Proof of Work, miners compete to produce blocks by computing hash functions to find a random number that satisfies certain conditions. To an external observer of the network, the total amount of hash power participating in this computation is impossible to know precisely. Each participant only knows their own computational power, but not that of others. Mathematical probability can give a rough estimate of how much hashing effort the successful miner likely expended to find a new block, but the true amount remains unknown. The random number included in the block thus serves as a kind of fuzzy “proof,” implying how much computational work the miner may have contributed to maintaining the longest chain they observe.
In Proof of Stake, however, the staked funds representing each validator’s weight are completely transparent. Validators must first deposit their funds before they can begin participating in consensus and earning rewards. When a validator casts a vote, other validators do not need to make uncertain guesses about its weight—they can simply check how much stake that validator has locked up.
So, where is the “Proof” in Proof of Stake?
This blog post isn’t meant to answer that question—the above paragraphs are little more than rambling thoughts. What I want to record and explore here is another crucial property of the Proof of Stake protocol: randomness.
“Randomness”
Proof of Work 用数学概率为矿工们找到属于自己的合适位置,你投入的算力占比决定了你挖出来的区块有多大的可能性被纳入到主网之中。而 Proof of Stake 中,验证者按照规划好的序列轮流获得出块权。如何决定出块序列成为 Proof of Stake 在摒弃了算力竞争之后必须要解决的问题。
按照序列轮流出块是一个自然的想法,这似乎也是 BNB Chain 所采用的方式。这样的简单直观为验证者带来的是清晰的规划,所有的验证者都知道自己会在什么时间点负责什么样的任务,他们对于其他的验证者也会有着明确的认知。这会为攻击者提供很多的信息,让他们更易于发动攻击。
基于这样的想法,Ethereum 采用的方法是随机生成。在以 epoch 为基本周期的规划中,当 epoch 1 开始时,算法会利用 epoch 0 中的信息,为 epoch 2 提供规划。
这一过程所采用的算法被称为 RANDAO,我们可以将其看作在一个 epoch 中累加随机性的工具。epoch 中每一个被提出的区块会为最终的结果提供一些助力。毕竟这样的随机性也需要共识,哪为什么不顺便将它和其他需要共识的东西塞到一起呢?
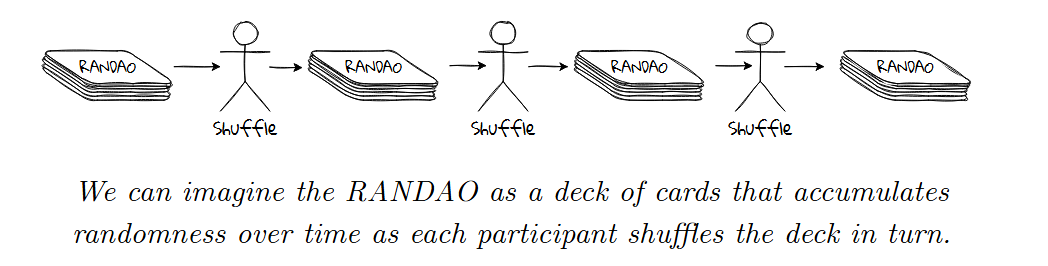
Actual Procedure
每一个 Ethereum 区块包含一个 randao_reveal 域,这一位置上的值按照如下步骤获得:
- 验证者用自己的私钥在 epoch 编号上签名
- 将第一步得到的结果进行哈希
- 将第二步得到的结果与上一个区块得到的 RANDAO 值进行按位异或运算
- 得到新的 RANDAO 值
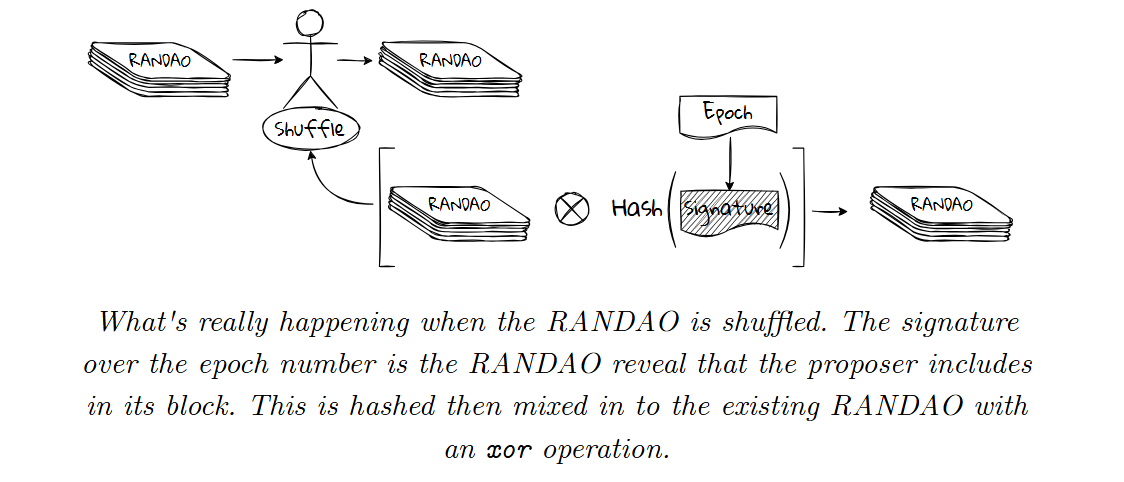
每一个存在于主链上的区块都会对 RANDAO 进行一次洗牌,对于缺失的 slot,他自然就不会发挥作用。这也意味着每一个 slot 的出块者都可以借用自己的身份让下一个 RANDAO 出现两种情况:1. 自己出块,带来一个新的 RANDAO;2. 自己不出块,让下一个出块者看到和当前一样的值。
只要一个 epoch 中存在至少一个 slot 的出块者正常出块,那么下一个 epoch 所用到的 RANDAO 值就是与上一个 epoch 不一样的。
RANDAO Unpredictability
由于每一个验证者的私钥是不公布的,哈希是不可逆的,每一个验证者都能为 RANDAO 的最终结果做出贡献,但作为参与者的他们也同样无法提前预测最终的结果。
噢,好像不完全是这样的:进行“洗牌“的最后一位验证者可以早于其他验证者获知结果,不是吗?
最后一位验证者知道他洗完的牌就是最终的结果了,因此他相较于其他验证者而言有一个额外的优势:他可以在自己可以获得的两种情况中选择对自己更有利的一方。
如果倒数第一位验证者和倒数第二位联合起来,他们具有的选择可能性就会变得更多。更进一步,如果位于 epoch 结尾的连续 k 个验证者相互串通,他们就具有 2^k 种选择可能性,他们可以自由的从中选择对自己最有利的结果。
Early Discussion
Upgrading Ethereum | 2.9.3 Randomness
Selfish Mixing and RANDAO Manipulation - Consensus - Ethereum Research
社区很早就认识到了 RANDAO 受影响的可能性,并对此进行了一定程度的分析。我这里给出的两个例子都考虑到了在 epoch 结束的连续 k 个 slot 被攻击者占据所能带来的危害。他们讨论了特定质押量占比的攻击者能借此获得的额外 slot 数量,以及持续占据某个指定位置的 slot 的几率。
特别的,eth2book.info 上对于占据连续的 k 个 slot 的情况偏理论分析,而 ethresear.ch 上以 Lido 作为样本给出了一个实际的例子。
对于获得指定位置的 slot 的分析上,eth2book.info 关注能否获取最后一个 slot,而 ethresear.ch 则考虑了更广泛的情况。这是因为前者更关注这个攻击的继续实现,后者则考虑了特殊事件对于攻击者的吸引力。
他们进行的概率计算,图表呈现大体十分相似,在细节上存在区别。
Extended with MDP
[2409.19883] Optimal RANDAO Manipulation in Ethereum
通过将单步的概率计算拓展为周期性的马尔可夫过程,Alpturer 和 Weinberg 计算得到了对 RANDAO 进行篡改的最优策略和相应结果。他们将攻击者在一个 epoch 中掌握的 slot 分为零散的和在尾部连续的,由此进行概率分布的建模并合并到马尔可夫模型中。
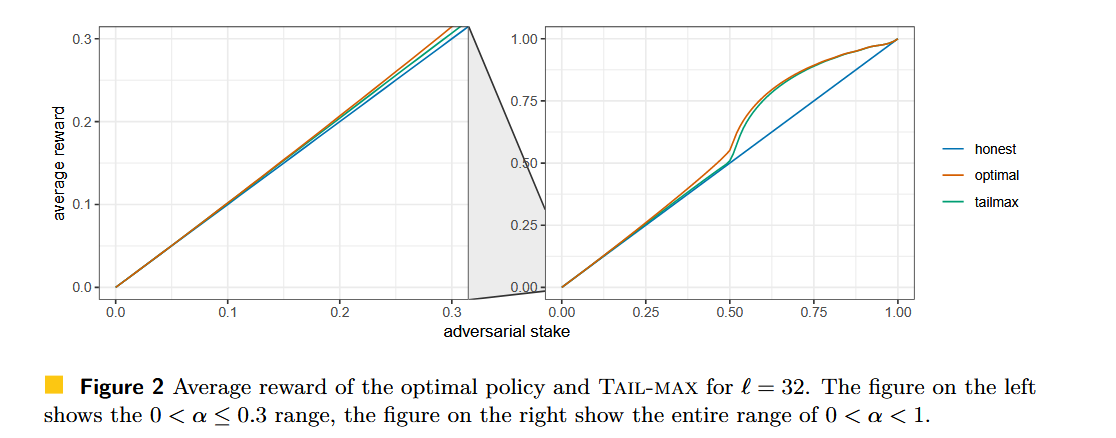
从结果上来看,即便是最优策略,能获得的期望收益也并未显著高于诚实的策略。
Extended with Forking
在 Forking the RANDAO: Manipulating Ethereum’s Distributed Randomness Beacon 中, Nagy 指出,攻击者在并未掌握尾部区块的前提下,可以通过 fork 诚实验证者的区块来选择更有利于自己的 RANDAO 结果。他们将这种情况和对应的策略加入到马尔可夫过程中,进一步降低了攻击的发动条件,他们得到的结果相比于前一篇工作有所提高,但都只在攻击者的质押占比较高时能为攻击者带来值得关注的额外收益。
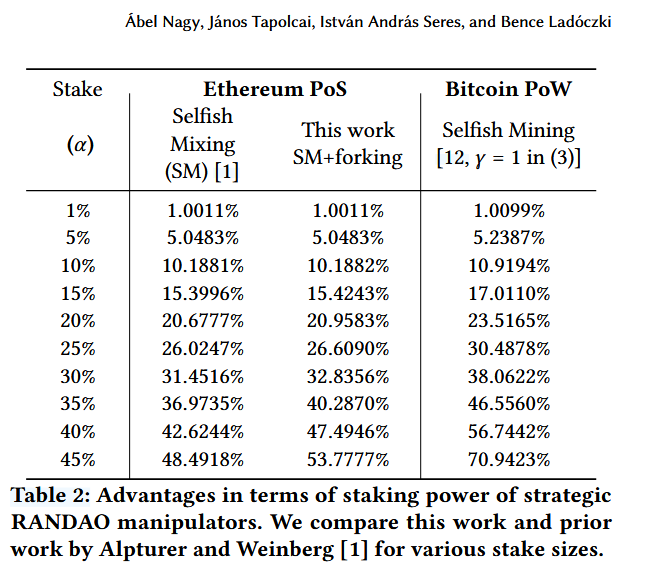
此外,他们对以太坊上进行的数据分析证明,这一攻击策略尚不存在实际实例。
Case I: Honest - Adversary - Honest | Adversary
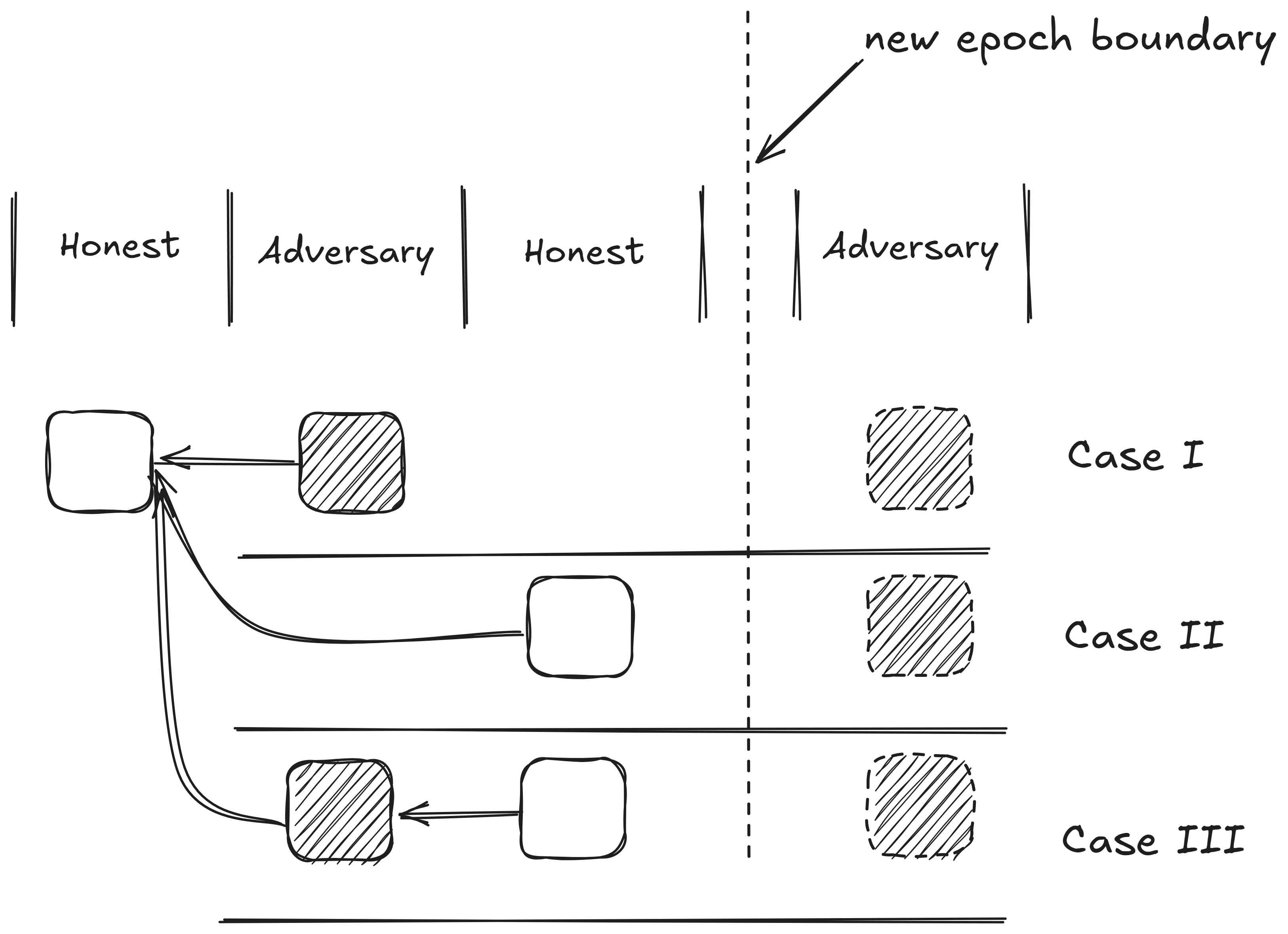
Case II: Honest - Adversary - Honest - Adversary |
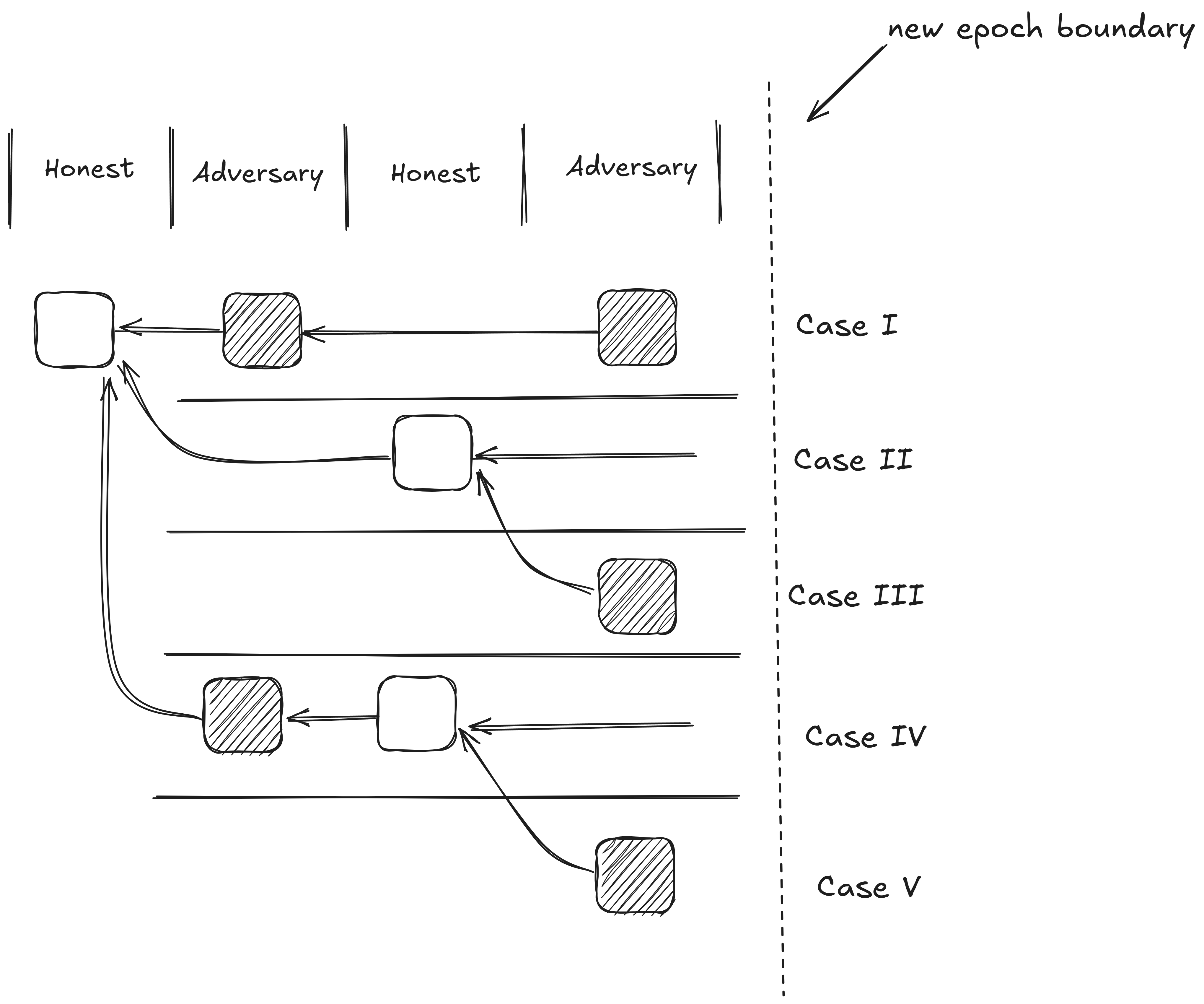
上面给出了论文提供用以解释这一策略的两种形式,他们的共同点都涉及到了两个攻击者的出块机会和一个诚实验证者的出块机会(假定攻击者的占比大于 0.2,诚实验证者的 proposer boost 为 0.4)。
由此,我们发现这一策略的加入为原本的 RANDAO mixing 扩展了额外的攻击空间,攻击者可以在更广泛的情形下操纵 RANDAO 以获取对自己有利的结果。但我们需要注意到的一点是:这里的策略并不如前面的 RANDAO mixing 一样具有更大的确定性。后者所有的可能性对于攻击者而言都是能够随意实现的。现在的策略下,虽然有这样多种的可能,但攻击者并不是能够任意的跳动到不同的时间线上。